Théorème d'échantillonnage de Shannon
De AgregmathKL
Révision de 1 décembre 2013 à 19:16 par Maxime Pouvreau (discuter | contributions)
Ce développement présente des propriétés du sous-espace des fonctions de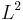 
dont la transformée de Fourier est à support compact. Le théorème a des applications en traitement du signal, même si on n'énonce que implicitement ici le résultat habituellement utilisé qui dit que la fréquence d'échantillonnage d'un signal doit être au moins égale au double de la fréquence maximale du signal.
Référence : Michel Willem, Analyse harmonique réelle.
Recasage :
- 201 -- Espaces de fonctions : exemples et applications.
- 205 -- Espaces complets. Exemples et applications.
- 207 -- Prolongement de fonctions. Exemples et applications. (utilisation de la transformée de Fourier sur 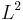, mais c'est peut-être un peu tordu)
- 208 -- Espaces vectoriels normés, applications linéaires continues. Exemples
- 213 -- Espaces de Hilbert. Bases hilbertiennes. Exemples et applications.
- (228 -- Continuité et dérivabilité des fonctions réelles d'une variable réelle. Exemples et contre-exemples.)
- 234 -- Espaces L^p, 1 ≤ p ≤ +∞.
- 239 -- Fonctions définies par une intégrale dépendant d'un paramètre. Exemples et applications.
- 240 -- Transformation de Fourier, produit de convolution. Applications.
- 246 -- Séries de Fourier. Exemples et applications.
