240 -- Produit de convolution, transformation de Fourier. Applications.
De AgregmathKL
(Redirigé depuis 240 -- Transformation de Fourier, produit de convolution. Applications.)
Sommaire
Plans
![]() Plan scanné de l'année 2013-2014
Plan scanné de l'année 2013-2014
![]() Plan scanné de l'année 2014-2015
Plan scanné de l'année 2014-2015
![]() Plan scanné de l'année 2015-2016
Plan scanné de l'année 2015-2016
Autre plan
Voici le plan que j'envisage:
Convolution
Définitions
Le cas général d'existence semble porter le nom de théorème de Young.
Régulariastion et approximation
On énonce un théorème qui dit que la convolée garde la régularité de la fonction la plus régulière. Approximations de l'unité. Théorèmes de densité.
Transformation de Fourier
Dans 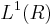 , lien avec la convolution. Formule sommatoire de Poisson
, lien avec la convolution. Formule sommatoire de Poisson
Dans l'espace de Schwartz, inversion, prolongement à 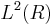
Application à l'équation de la chaleur
Extension de la transformation de Fourier aux distributions tempérées
Définition de l'espace 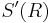
Transformation de Fourier dans 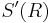 , applications à la résolution d'une EDP
, applications à la résolution d'une EDP
Rien de bien original, certes.
Commentaires
Selon Laurent Guillopé (jury aux oraux blancs), il faut savoir calculer la transformée de Fourier :
- d'une fonction constante ;
- d'une fonction créneau (fontion caractéristique de
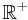 ) : cela donne l'exemple d'une fonction analytique non
) : cela donne l'exemple d'une fonction analytique non 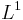 ;
; - de la Gaussienne ;
- de
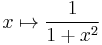 ;
; - de
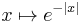 (ces deux dernières étant reliées).
(ces deux dernières étant reliées).
Leçon remplacées en 2016 par la 250 -- Transformation de Fourier. Applications