239 -- Fonctions définies par une intégrale dépendant d'un paramètre. Exemples et applications.

Plans

Plan scanné de l'année 2012-2013

Plan scanné de l'année 2013-2014

Plan scanné de l'année 2014-2015

Plan scanné de l'année 2015-2016

Plan scanné de l'année 2016-2017

Plan scanné de l'année 2017-2018

Plan scanné de l'année 2018-2019

Plan scanné de l'année 2019-2020

Plan scanné de l'année 2020-2021

Autre plan

Je vous propose ce que l'on avait fait quand nous (Alan Hertgen et Florent Demeslay) avions préparé notre leçon :

Régularité

[ZQ]

Théorèmes de

• continuité ;
• dérivabilité avec contre-exemple construit par Adrien Richou pour montrer la petite subtilité avec le presque partout dans le théorème de dérivabilité ;
• holomorphie.

Etude asymptotique :

• Méthode de Laplace ;
• Phase stationnaire ;
• Lemme de Van der Corput. [CL]

Théorie de Cauchy

[Rud]

Intégration sur un chemin, indice, formule de Cauchy et théorème des résidus.

Convolution

[Bre]

Fonctions convolables, suites régularisantes, fonctions plateaux, converge uniforme et 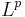$L^{p}$.

Transformée de Fourier

[ZQ]

Dans le cadre 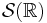${\mathcal {S}}({\mathbb {R}})$ exclusivement : définition, isomorphisme, formule d'inversion, formule sommatoire de Poisson, application aux EDP.

Développements possibles

[ZQ]

• Prolongement de 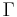$\Gamma$ avec formule d'Euler (à télécharger : Média:ProlongementGamma.tex)
• Méthode de Laplace
• Formule sommatoire de Poisson + 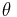$\theta$ de Jacobi
• Théorème d'échantillonnage de Shannon

Références

• [ZQ] Zuily-Quéffelec : Analyse pour l'Agrégation
• [Bre] Brézis : Analyse fonctionnelle
• [Rud] Rudin : Analyse réelle et complexe
• [CL] Chambert-Loir : Analyse 2

Développements

• Méthode de Laplace
• Intégrale de Fresnel
• Théorème d'échantillonnage de Shannon
• Formule d'inversion de Fourier