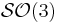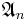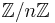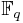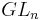Développements : Différence entre versions

Version du 2 novembre 2011 à 12:15

Certains d'entre nous tapent leurs développements. Vous pouvez, en plus des liens mis dans les pages leçons, les rassembler ici.

Pensez à ajouter les sources de vos développements : bien utile parfois !

Développements d'algèbre

Sous groupes finis de

Groupe circulaire

Ellipse de Steiner

Commutant d'un endomorphisme. (Gwen : J'ai remplacé l'ancienne version par une moins succincte)

Groupes d'ordre 12

Simplicité de

Caratheodory (and co)

Sylow

Automorphismes de

Polynômes irréductibles sur

Décomposition de Dunford et application à 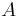diagonalisable 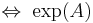diagonalisable

Théorème de l'élément primitif

Théorème de Hahn-Banach en dimension finie

Une version faible du théorème de Dirichlet

Réduction des matrices normales

Développements d'analyse

Méthode de Laplace

Prolongement de la fonction

Bernoulli et développement dyadique

Ruine du joueur

Ellipsoïde de John-Loewner

Le théorème de Weierstrass (via les polynômes de Bernstein)

-> Le même résultat en passant par les probabilités : ( .tex, .pdf)

Le théorème de Glaeser

Lemme de Morse

Théorème de Brouwer en dimension 2

Lemme de Borel

Théorème d'Abel angulaire

Un exemple de calcul d'intégrale

Théorème de Cauchy-Arzela-Peano

Critère de Weyl

Dérivée des fonctions lipschitziennes

Formule des compléments

Théorème de stabilité de Lyapounov

Méthode de Gauss d'approximation d'intégrale

Développements mixtes

Lie-Kolchin

Surjectivité de l'exponentielle

Simplicité de SO(3)

Sous-groupes compacts de

Théorème de Cartan Von Neumann

Convergence de la méthode de gradient à pas optimal (+Kantorovitch)

Théorème de Müntz ( Source .tex ; .pdf)

Ellipsoïde de John-Lœwner ( Source .tex ; .pdf)

Développements informatique

Langage de pile d'un automate à pile ( Source .tex ; .pdf)