Exos classiques et autres démonstrations
De AgregmathKL
Révision de 21 juin 2013 à 10:39 par Simon Boulier (discuter | contributions) (→Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage)
Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage
Soit 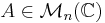 .
soit
.
soit 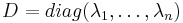 telle que
telle que 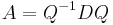 .
Soit
.
Soit 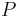 un polynôme tel que
un polynôme tel que 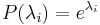 pour tout
pour tout 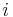 .
Alors
.
Alors 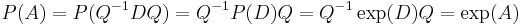 !
!