Le paradoxe de Banach-Tarski : Différence entre versions
De AgregmathKL
| Ligne 13 : | Ligne 13 : | ||
* [[101 -- Groupe opérant sur un ensemble. Exemples et applications.]] | * [[101 -- Groupe opérant sur un ensemble. Exemples et applications.]] | ||
* [[183 -- Utilisation des groupes en géométrie.]] | * [[183 -- Utilisation des groupes en géométrie.]] | ||
| + | |||
| + | |||
| + | |||
| + | [[Category:Développement de la leçon 101]] | ||
| + | [[Category:Développement de la leçon 183]] | ||
Version actuelle en date du 16 décembre 2014 à 15:12
Le paradoxe de Banach-Tarski est un résultat contre-intuitif sur la géométrie dans l'espace qui dérive de l'axiome du choix. Ce développement se propose de montrer une version faible qui stipule que la sphère unité privée d'un ensemble dénombrebable de points peut être découpée en un nombre fini de parties qui peuvent être assemblées via des rotations vectorielles en l'union disjointe de deux sphères unité privées du même ensemble.
Le même résultat généralisé pour les boules (sans retirer de points cette fois) montre que la notion de volume n'est pas définie pour toute partie de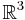 
: Il existe des parties non lebesgue-mesurables.
Le développement
Références
Principalement le RMS 118 n°3.
