Exos classiques et autres démonstrations : Différence entre versions
De AgregmathKL
| Ligne 15 : | Ligne 15 : | ||
== Pseudo-réduction simultanée == | == Pseudo-réduction simultanée == | ||
| − | [[Fichier:Pdf.png|alt=Pdf|link=Média:Pseudored.pdf|24px]] | + | [[Fichier:Pdf.png|alt=Pdf|link=Média:Pseudored.pdf|24px]][[Fichier:Tex.png|alt=Tex|link=Média:Pseudored.tex|24px]] |
| − | + | ||
| − | [[Fichier:Tex.png|alt=Tex|link=Média:Pseudored.tex|24px]] | + | |
== Racine carrée d'une matrice symétrique réelle positive == | == Racine carrée d'une matrice symétrique réelle positive == | ||
[[Fichier:Pdf.png|alt=Pdf|link=Média:RacinecarreeSn.pdf|24px]] | [[Fichier:Pdf.png|alt=Pdf|link=Média:RacinecarreeSn.pdf|24px]] | ||
| − | |||
[[Fichier:Tex.png|alt=Tex|link=Média:RacinecarreeSn.tex|24px]] | [[Fichier:Tex.png|alt=Tex|link=Média:RacinecarreeSn.tex|24px]] | ||
| Ligne 30 : | Ligne 27 : | ||
[[Fichier:Pdf.png|alt=Pdf|link=Média:Projecteurs.pdf|24px]] | [[Fichier:Pdf.png|alt=Pdf|link=Média:Projecteurs.pdf|24px]] | ||
| − | |||
[[Fichier:Tex.png|alt=Tex|link=Média:Projecteurs.tex|24px]] | [[Fichier:Tex.png|alt=Tex|link=Média:Projecteurs.tex|24px]] | ||
| Ligne 36 : | Ligne 32 : | ||
[[Fichier:Pdf.png|alt=Pdf|link=Média:Diagocommut.pdf|24px]] | [[Fichier:Pdf.png|alt=Pdf|link=Média:Diagocommut.pdf|24px]] | ||
| − | |||
[[Fichier:Tex.png|alt=Tex|link=Média:Diagocommut.tex|24px]] | [[Fichier:Tex.png|alt=Tex|link=Média:Diagocommut.tex|24px]] | ||
| Ligne 42 : | Ligne 37 : | ||
[[Fichier:Pdf.png|alt=Pdf|link=Média:Polsymetriques.pdf|24px]] | [[Fichier:Pdf.png|alt=Pdf|link=Média:Polsymetriques.pdf|24px]] | ||
| − | |||
[[Fichier:Tex.png|alt=Tex|link=Média:Polsymetriques.tex|24px]] | [[Fichier:Tex.png|alt=Tex|link=Média:Polsymetriques.tex|24px]] | ||
= Analyse = | = Analyse = | ||
Version du 24 juin 2013 à 23:18
Sommaire
- 1 Algèbre
- 1.1 Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage
- 1.2 Pseudo-réduction simultanée
- 1.3 Racine carrée d'une matrice symétrique réelle positive
- 1.4 Calcul des projecteurs sur les sous-espaces caractéristiques d'un endomorphisme
- 1.5 Une famille d'endomorphismes diagonalisables qui commutent est codiagonalisable
- 1.6 Expression d'un polynôme symétrique en fonction des polynômes symétriques élémentaires
- 2 Analyse
Algèbre
Calculer l'exponentielle d'une matrice diagonalisable sans calculer la matrice de passage
Soit 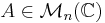 .
soit
.
soit 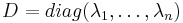 telle que
telle que 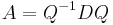 .
.
Soit 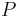 un polynôme tel que
un polynôme tel que 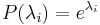 pour tout
pour tout 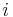 .
.
Alors 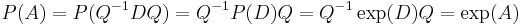 !
!
Ref : perso.univ-rennes1.fr/tristan.vaccon/exponentielle_de_matrices.pdf
Pseudo-réduction simultanée
Racine carrée d'une matrice symétrique réelle positive
Calcul des projecteurs sur les sous-espaces caractéristiques d'un endomorphisme
On donne ici une méthode pour calculer les projecteurs sur les sous-espaces caractéristiques d'un endomorphismes, ainsi qu'une application au calcul de l'exponentielle matricielle par la décomposition de Dunford.