249 -- Suites de variables de Bernoulli indépendantes.
Plans
![]() Plan scanné de l'année 2012-2013
Plan scanné de l'année 2012-2013
![]() Plan scanné de l'année 2013-2014
Plan scanné de l'année 2013-2014
![]() Plan scanné de l'année 2014-2015
Plan scanné de l'année 2014-2015
![]() Plan scanné de l'année 2015-2016
Plan scanné de l'année 2015-2016
Commentaires
Éléments presque sûrement indispensables :
- Absence de i avant les deux « l » dans Bernoulli.
- Loi de Bernoulli, évidemment, qui appelle les loi binomiale et géométrique. (Et pourquoi pas les lois de Rademacher et loi hypergéométrique.)
- L'indépendance, qui figure dans l'intitulé de la leçon, est à mon avis un concept subtil qui mérite d'être exposé, même si la sous-partie en question ne contient qu'essentiellement des définitions. Donner le Lemme de Borel-Cantelli me paraît quasi-obligatoire, dans la mesure où c'est un outil fondamental pour démontrer les lois des grands nombres (en plus ça permet d'évoquer la loi du 0-1 de Kolmogorov, qui est quand même très jolie.) Remarquer que l'indépendance globale est plus forte que l'indépendance "n à n".
- Les lois des grands nombres parce qu'elles confirment l'intuition naturelle qu'on a pour une infinité de lancers de piles ou faces. Pour des variables de Bernoulli indépendantes, la loi faible se retrouve rapidement en écrivant l'inégalité de Tchebytchev. C'est pour cela qu'on a choisi de l'énoncer avec les hypothèses
- Variables
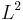 deux à deux non-corrélées,
deux à deux non-corrélées, 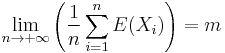 ,
,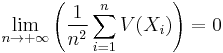 plutôt que
plutôt que - Variables
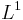 identiquement indépendantes
identiquement indépendantes
En effet la preuve de 1. repose sur l'inégalité de Tchebytchev, et la 2. en est un corollaire. (cf. Ouvrard.)
Autres éléments qui peuvent avoir leur place dans le plan
Construire une suite de variables de Bernoulli indépendantes
L'existence d'une suite de variable aléatoires indépendantes de lois données n'est pas triviale. C'est l'objet du théorème de prolongement de Kolmogorov. On trouve dans l'Ouvrard une construction à partir de la mesure de Lebesgue sur [0,1) qui passe par des Bernoulli. En bonus on obtient des mesures étrangères à Lebesgue et diffuses (c.-à-d. qui ne chargent aucun point.) Je trouve que c'est en plein dans la leçon, les preuves sont élémentaires et belles. (Personnellement je pense même que ça fait un bon développement.)
Le Théorème de la limite Centrale
Historiquement, le premier TCL a été prouvé pour des Bernoulli (Théorème de Moivre-Laplace) : voilà une belle manière d'introduire le TCL dans cette leçon. On peut en parler notamment pour donner un intervalle de confiance approximatif pour l'estimateur du paramètre de la loi de Bernoulli. Le théorème de Berry-Esséen donne une majoration de l'erreur commise en faisant cette approximation : chouette non ? (C'est peut-être l'occasion de parler de statistiques à moindre coût.)
Plus de statistiques
Le théorème de Glivenko-Cantelli donne la convergence uniforme p.s. des fonctions de répartition empiriques vers la fonction de répartition de la loi des variables identiquement indépendantes considérées. Les fonctions de répartition empiriques sont des sommes d'indicatrices, qui sont toujours des variables de Bernoulli. On peut penser aussi au théorème de Varadarajan, qui lui donne la convergence étroite des mesures empiriques, et qui prends parfois le nom de "principe fondamental de la statistique". La seule référence qu'on ait trouvé à ce propos est le premier chapitre du cours de statistiques de Benoît Cadre.
Chaînes de Markov
Mentionner la marche aléatoire sur 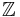 permet d'introduire les chaînes de Markov. On peut alors énoncer que cette marche aléatoire est récurrente si et seulement si la loi de Bernoulli est uniforme. En marchant aléatoirement (et uniformément) sur
permet d'introduire les chaînes de Markov. On peut alors énoncer que cette marche aléatoire est récurrente si et seulement si la loi de Bernoulli est uniforme. En marchant aléatoirement (et uniformément) sur 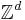 , on peut énoncer le théorème de Polya, qui dit que la marche est récurrente si et seulement si
, on peut énoncer le théorème de Polya, qui dit que la marche est récurrente si et seulement si 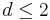 .
La loi de l'arcsinus ( voir cette sympathique vidéo trouvée sur images des maths pour une introduction ) a sa place une fois qu'on a parlé de marche aléatoire sur
.
La loi de l'arcsinus ( voir cette sympathique vidéo trouvée sur images des maths pour une introduction ) a sa place une fois qu'on a parlé de marche aléatoire sur 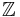 (voir Lesigné).
(voir Lesigné).
Martingales
La marche aléatoire sur  peut être vue comme un modèle pour la ruine du joueur. L'occasion d'introduire la notion de martingale, si on est à l'aise avec la notion d'espérance conditionnelle.
peut être vue comme un modèle pour la ruine du joueur. L'occasion d'introduire la notion de martingale, si on est à l'aise avec la notion d'espérance conditionnelle.
Développements possibles
- Autour du développement dyadique : construction d'une suite indépendante de variables de loi quelconque et mesures singulières en bonus (Ouvrard p. 52).
- Théorème de Weierstrass via les polynômes de Bernstein. (Zuily-Queffelec) ( .tex, .pdf)
- Grandes déviations pour les bernoulli. (Lesigné)
- Théorème de Polya.
- Ruine du joueur. (Ouvrard)
- Processus de Galton-Watson.
Références
- Ouvrard
- Barbe-Ledoux
- Zuily-Queffélec
- Emmanuel Lesigné, "Pile ou Face : Une introduction aux théorèmes limites du Calcul des Probabilités" : ce petit livre est une mine d'or pour cette leçon, et pour cause : l'auteur se propose d'introduire les probabilités uniquement en considérant des Bernoulli (!) En réalité il va très loin, traite notamment les "grandes déviations" pour les Bernoulli, mais aussi la loi du log itéré, celle de l'arcsinus, et plein d'autres choses marrantes.
--Nil 19 mai 2011 à 22:26 (CEST)