208 -- Espaces vectoriels normés, applications linéaires continues. Exemples.

Plans

Plan scanné de l'année 2012-2013

Plan scanné de l'année 2013-2014

Plan scanné de l'année 2014-2015

Plan scanné de l'année 2016-2017

Plan scanné de l'année 2017-2018

Plan scanné de l'année 2018-2019

Plan scanné de l'année 2019-2020

Plan scanné de l'année 2020-2021

Développements

• Théorème de Banach-Steinhaus et application aux séries de Fourier
• Théorème d'échantillonnage de Shannon

Exercices posés lors de la présentation

Exercices proposés en 2013

Divers

Quelques remarques qui me paraissent pertinentes : (Nil)

Définir un espace vectoriel normé ?

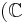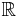Dans [N. Bourbaki, Topologie Générale, IX, p. 29] on apprend qu'il suffit que l'espace vectoriel soit sur un corps muni d'une valeur absolue pour définir une norme. C'est donc une notion qui s'étend au delà des $({\mathbb {C}}$ ou ${\mathbb {R}}$)-espaces vectoriels. Par exemple, on peut définir des 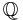${\mathbb Q}$-espaces vectoriels normés, mais aussi des 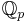${\mathbb {Q}}_{p}$-espaces vectoriels normés, où les 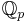${\mathbb {Q}}_{p}$ désignent les corps p-adiques : définir les EVN avec cette généralité me paraît donc tout à fait dangereux. 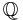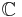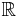En revanche, parler de ${\mathbb Q}$-espaces vectoriels normés permet d'éclairer certains résultats, qui sont vrais sur ${\mathbb {C}}$ ou ${\mathbb {R}}$ mais pas sur 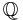${\mathbb Q}$, parce que la complétude interviens dans la preuve. (En dimension finie : La complétude bien sûr, mais aussi l'équivalence de toutes les normes, et probablement également la continuité automatique des applications linéaires (à vérifier)).

Situer les EVN dans le paysage topologique

La norme est une manière simple de répondre à la question : "Comment fabriquer une topologie sur un EV qui rende continues les opérations ?". Tout Espace vectoriel sur un corps muni d'une valeur absolu peut être muni d'une norme (Voici une idée de preuve donnée par Christophe Cheverry : Tout Espace vectoriel 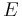$E$ admet une base algébrique 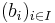$(b_{i})_{{i\in I}}$, d'où 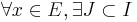$\forall x\in E,\exists J\subset I$ fini tel que 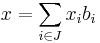$x=\sum _{{i\in J}}x_{i}b_{i}$. On pose alors 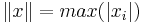$\|x\|=max(|x_{i}|)$ ). Noter quand même que l'existence d'une base algébrique est une conséquence de l'axiome du choix). Pour autant, toute topologie d'espace vectoriel n'est pas issue d'une norme. En contre-exemple, on peut penser, par décroissance de risque à mon avis, à de la topologie faible et à de la topologie d'espace vectoriel localement convexe (Issue d'une famille de semi-normes, en particulier pas forcément séparée : c'est peut être pas mal puisque les distributions sont au programme maintenant.) L'exemple le moins dangereux qu'on ait trouvé est 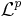${\mathcal L}^{p}$ muni de sa semi-norme, qui n'est pas séparé. (1)

(1) note de SB : je suppose qu'il s'agit de l'exemple "consistant" le moins dangereux. Parce que sinon la topologie grossière convient : elle rend continue tout le monde, donc munit bien n'importe quel e.v. d'une structure d'e.v.t. Je retourne tout de suite voir LMB. :-)

Et mes remarques (toujours SB) : franchement les Q_p-normes c'est pipô (aucun jury ne viendra nous ennuyer dessus) et je pense aussi que la question de la normabilité d'un e.v. est un peu pathologique. Ou alors ils sont bizarres dans les jurys, il y a quand même des maths qui "font sens" (c'est un anglicisme, je sais) un peu plus...