182 -- Applications des nombres complexes à la géométrie.
De AgregmathKL
Sommaire
Plans
![]() Plan scanné de l'année 2012-2013
Plan scanné de l'année 2012-2013
![]() Plan scanné de l'année 2013-2014
Plan scanné de l'année 2013-2014
![]() Plan scanné de l'année 2014-2015
Plan scanné de l'année 2014-2015
![]() Plan scanné de l'année 2015-2016
Plan scanné de l'année 2015-2016
![]() Plan scanné de l'année 2016-2017
Plan scanné de l'année 2016-2017
![]() Plan scanné de l'année 2017-2018
Plan scanné de l'année 2017-2018
![]() Plan scanné de l'année 2018-2019
Plan scanné de l'année 2018-2019
Autre plan
1. Bases (tellement la ~)
- Géométrie euclidienne affine
- Définitions : affixe, vecteur image. Liens entre la structure hermitienne de
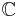 et la géométrie.
et la géométrie. - Applications : colinéarité, équations de droites et de cercles.
- Définitions : affixe, vecteur image. Liens entre la structure hermitienne de
- Angles et coordonnées polaires [Aud]
- Isomorphisme de groupe
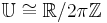
- Applications : Théorème de l'angle inscrit ? Ptolémé
- Isomorphisme de groupe
- Transformations
- Isométries directes
- Isométries puis similitudes
- App : Développé de la cycloïde [Arn]
- Polynômes et barycentres
- Applications : Théorème de Gauss-Lucas
- DEV : Ellipse de Steiner.
2. Droite projective complexe
- DéfinitionS
- Définitions équivalentes [Cos]
- Exemple : projection stéréographique [Aud]
- Homographies [Aud, Cos]
- Groupe et ses générateurs
- Application : points fixes et suites homographiques [Cos]
- Birapport [Aud, Eid]
- Applications : Cocyclicité, Premutation et birapport [Aud], Alternative de Steiner
- Groupe circulaire [Aud]
- DEV : Action du groupe circulaire
- Fibration de Hopf [Dim, Cer]
Développements
- Ellipse de Steiner
- Action du groupe circulaire sur la sphère de Riemann
- Fibration de Hopf ?
- Théorème de Jordan
- Théorème de Gauß pour les polygones réguliers constructibles
- Action du groupe modulaire sur le demi-plan de Poincaré
Références
- [Aud] : Audin (3ième édition)
- [Gob] : Goblot
- [Eid] : Eiden
- [Arn] : Lelong-ferrand Arnaudiès, Géométrie et cinématique Tome 3
- [Cos] : Cours de M. Coste
- [Dim] : Film dimension
- [Cer] : Cours de D. Cerveaux