919 -- Unification : algorithmes et applications.
De AgregmathKL
Révision de 3 juin 2012 à 10:59 par Basile (discuter | contributions) (→Plan Basile et Kévin (2012))
"Rien"
Le jury (s'il était unifié à {LMB}).
Plan Basile et Kévin (2012)
Le plan
Intro : motivation de l'intérêt de l'unification pour le typage. Exemple avec Ocaml.
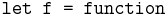
![\;{\texttt {|\ []\ ->\ (fun\ y\ ->\ [y])}}](/images/math/f/c/c/fcc2ac43c7f524ed59eca4a682101310.png)
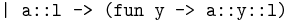
I - Unification
Langage du premier ordre et termes.
On se donne une famille d'ensemble de symboles de fonctions (dits d'arité 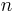 ) :
) : 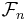 pour
pour 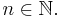 .
On pose
.
On pose 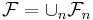 .
Et on considère un ensemble infini
.
Et on considère un ensemble infini 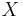 de symboles de variables.
de symboles de variables.
- Definition
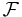 -algèbre : ensemble + interpréation pour tous les symboles de fonctions.
-algèbre : ensemble + interpréation pour tous les symboles de fonctions. - Definition
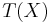 ensemble des termes à variable dans
ensemble des termes à variable dans 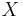 par induction.
par induction. - C'est une
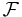 -algèbre.
-algèbre. - Les termes clos sont les éléments de
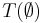 .
. - Définition annexes (par induction) : positions, variables.
- Exemple.
Substitutions
- Propriété universelle des termes clos, propriété universelle des termes (liberté).
- Corollaire définition : existence des substitutions.
- Définitions annexes : domaine, portée d'une substitutions.
- Exemple
Unification
- Problème d'unification. notation.
- Définition unificateur, ordre
- Unificateur principal
- Problème de correspondance/filtrage.
II - Algorithmes
- Naïf
- Celui de Stern
- Celui de AllThat (si différent)
- Evolué
- Union-find et termes en DAG (AllThat)
- Developpement : Algorithme d'unification
- Union-find et termes en DAG (AllThat)
III - Applications
Réécriture
- Definitions SRT
- Confluence locale
- Lemme de Newman
- Developpement : Lemme des paires critiques (AllThat)
Logique
- Méthode de résolution
- Developpement : Complétude de la méthode de résolution (Stern)
- Le langage Prolog
Typage et filtrage
Développements Possibles
Proposés
Possibles
Références
- Baader, Nipkow : Term Rewriting and All That
- J. Stern : Fondements mathématiques de l'informatique
- Weis, Leroy : Le langage Caml