242 -- Utilisation en probabilités de la transformation de Fourier ou de Laplace et du produit de convolution. : Différence entre versions
| Ligne 1 : | Ligne 1 : | ||
| + | = Plan = | ||
| + | |||
| + | [[Fichier:Pdf.png|alt=Pdf|link=Média:242_2012-2013.pdf|24px]] [[Média:242_2012-2013.pdf | Plan scanné de l'année 2012-2013]] | ||
| + | |||
| + | |||
| + | = Autre = | ||
| + | |||
Depuis le temps que je devais le faire, je vous propose les commentaires que j'ai évoqué à l'oral, ainsi que quelques remarques. (Les détails peuvent sembler insultants, mais c’est pour que cela puisse éventuellement servir à ceux qui ne font pas l’option proba) | Depuis le temps que je devais le faire, je vous propose les commentaires que j'ai évoqué à l'oral, ainsi que quelques remarques. (Les détails peuvent sembler insultants, mais c’est pour que cela puisse éventuellement servir à ceux qui ne font pas l’option proba) | ||
| Ligne 47 : | Ligne 54 : | ||
(1) Caractérisation de l’indépendance) | (1) Caractérisation de l’indépendance) | ||
| − | On obtient un critère d’indépendance de variables aléatoires en terme de fonctions caractéristiques (juste un mot de la démonstration : on montre au préalable que la transformée de Fourier du produit tensoriel de deux mesures est le produit des transformée de Fourier des mesures, le reste utilise Fubini et le théorème d’injectivité ( [OUVRARD] p106 et [Barbe-LEDOUX] p80)). On notera que l’on considère la fonction caractéristique d’un n-uplet de variables aléatoire, il fallait donc la définir dans <math>Rd</math>. Ce résultat sert beaucoup en pratique, à commencer avec la proposition qui suit qui donne une caractérisation de l’indépendance de variables aléatoires réelles bornées (l’hypothèse bornée donne , dans la démonstration, que la famille est sommable). On peut montrer que l’hypothèse bornée n’est pas nécessaire avec un exemple un peu adhoc que je n’ai pas mis dans le plan : pour <math>X | + | On obtient un critère d’indépendance de variables aléatoires en terme de fonctions caractéristiques (juste un mot de la démonstration : on montre au préalable que la transformée de Fourier du produit tensoriel de deux mesures est le produit des transformée de Fourier des mesures, le reste utilise Fubini et le théorème d’injectivité ( [OUVRARD] p106 et [Barbe-LEDOUX] p80)). On notera que l’on considère la fonction caractéristique d’un n-uplet de variables aléatoire, il fallait donc la définir dans <math>Rd</math>. Ce résultat sert beaucoup en pratique, à commencer avec la proposition qui suit qui donne une caractérisation de l’indépendance de variables aléatoires réelles bornées (l’hypothèse bornée donne , dans la démonstration, que la famille est sommable). On peut montrer que l’hypothèse bornée n’est pas nécessaire avec un exemple un peu adhoc que je n’ai pas mis dans le plan : pour <math> X = Y </math> qui suit une loi de Cauchy on a la propriété qui est vérifié mais <math>X</math> n’est pas indépendante d’elle même (car les seules variables aléatoires indépendantes d’elle-même sont les constante ps). Une deuxième application est la caractérisation de l’indépendance des composantes d’un vecteur gaussien (ce qui est faux dans le cadre non gaussien car cela voudrait dire que l’indépendance est caractérisée par la non corrélation). |
(2) Loi de la somme de deux variables aléatoires indépendantes) | (2) Loi de la somme de deux variables aléatoires indépendantes) | ||
| Ligne 75 : | Ligne 82 : | ||
| − | [[ | + | [[Category:Leçon d'analyse]] |
| − | + | [[Category:Anciennes leçons]] | |
| − | [[Category: | + | |
Version du 21 avril 2022 à 21:46
Plan
![]() Plan scanné de l'année 2012-2013
Plan scanné de l'année 2012-2013
Autre
Depuis le temps que je devais le faire, je vous propose les commentaires que j'ai évoqué à l'oral, ainsi que quelques remarques. (Les détails peuvent sembler insultants, mais c’est pour que cela puisse éventuellement servir à ceux qui ne font pas l’option proba)
(Introduction)
Je pense qu'il est bon d'insister sur le fait qu'en théorie des probabilités, les principales questions concernant l'étude de variables aléatoires sont :
I Quelle est la loi ?
II Il y a-t-il indépendance ?
III Quel est le comportement asymptotique ?
ce qui justifie le plan suivit (l'ordre de ces questions est usuel), le but étant d'illustrer l'importance des outils (le titre de la leçon est d'ailleurs "utilisation...") que sont la transformée de Fourier (ou de Laplace) et le produit de convolution (ils se doivent donc d'apporter des résultats suivants chacun des axes proposés). On peut par la suite dire un mot sur la finalité : l'intérêt réside essentiellement dans le fait que la transformée de Fourier nous permet de calculer facilement la loi de la somme de variables aléatoires indépendantes qui apparaissent dans de nombreux théorèmes limites en particulier la LGN (la faible) et son TCL (pour citer les plus importants).
(Partie I : Caractérisation de la loi d'une variable aléatoire)
(1) Transformée de Fourier)
On rappelle oralement que la fonction caractéristique d'une variable aléatoire c'est sa transformée de Fourier (j'insiste sur le fait que ces rappels doivent être bref, comme il s'agit "d'utilisation...", il ne faut pas se focaliser sur la définition et les propriétés de bases, ce qui constituerai presque un cours sur la transformée de Fourier, ce qui n'est pas le but. Il faut vraiment mettre rapidement en avant le théorème d'injectivité, qui est fondamental car justifie tout ce qui suit, il se doit donc apparaître en premier). Il faut bien donner la définition dans 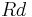 , puisque cela sert pour caractériser la loi d'un couple et pour l'indépendance. .On peut préciser que cette définition ne dépend que de la loi de
, puisque cela sert pour caractériser la loi d'un couple et pour l'indépendance. .On peut préciser que cette définition ne dépend que de la loi de 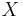 (ça a son importance !) et que comme son nom l'indique, elle caractérise la loi, ce qui permet d'enchaîner sur le théorème d'injectivité.
Ce théorème est fondamentale car il légitime :
-l'étude sur l'indépendance par la caractérisation donnée en Partie II
-l'étude sur le comportement asymptotique par la caractérisation de la convergence en loi, et les démonstration des théorèmes limites donnée en Partie III.
On peut commenter ce théorème : on sait que la donnée des
(ça a son importance !) et que comme son nom l'indique, elle caractérise la loi, ce qui permet d'enchaîner sur le théorème d'injectivité.
Ce théorème est fondamentale car il légitime :
-l'étude sur l'indépendance par la caractérisation donnée en Partie II
-l'étude sur le comportement asymptotique par la caractérisation de la convergence en loi, et les démonstration des théorèmes limites donnée en Partie III.
On peut commenter ce théorème : on sait que la donnée des 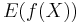 pour toutes fonctions boréliennes bornée détermine la loi de X. Le théorème d'injectivité nous assure qu'il suffit de montrer l'égalité des espérances pour les fonctions de la forme
pour toutes fonctions boréliennes bornée détermine la loi de X. Le théorème d'injectivité nous assure qu'il suffit de montrer l'égalité des espérances pour les fonctions de la forme 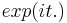 , ce qui permet de remplacer la classe des fonctions boréliennes bornés par la famille des fonctions sinus et cosinus.
Un petit mot de la démonstration (qui est difficile), on peut procéder de deux manières :
-utilisation du théorème des classes monotone fonctionnelle ([Barbe-Ledoux])
-utilisation des propriétés du noyau gaussien (c'est une démonstration plus "à la main")([Ouvrard])
, ce qui permet de remplacer la classe des fonctions boréliennes bornés par la famille des fonctions sinus et cosinus.
Un petit mot de la démonstration (qui est difficile), on peut procéder de deux manières :
-utilisation du théorème des classes monotone fonctionnelle ([Barbe-Ledoux])
-utilisation des propriétés du noyau gaussien (c'est une démonstration plus "à la main")([Ouvrard])
Autres remarques :
On notera que la transformée de Fourier peut se définir de la même manière pour des mesures finies (et pas seulement des mesures de probabilité). Concernant le cas où 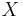 est une variable aléatoire à densité f, on retrouve la (presque, tout dépend de la définition) transformée de Fourier de
est une variable aléatoire à densité f, on retrouve la (presque, tout dépend de la définition) transformée de Fourier de 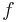 (pas de souci pour l'existence car
(pas de souci pour l'existence car 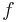 est dans
est dans 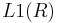 ).
Ensuite on peut justifier l'utilité des formules d'inversion qui suivent en disant que la transformée de Fourier ne permet pas (au même titre que la fonction de répartition ou la densité (quand elle existe)) de calculer des probabilités.
Les démonstration de ces formules d'inversion se font facilement avec Fubini.
La proposition que suit établit une relation entre les propriétés de dérivabilité de la fonction caractéristique et l'existence de moment d'une variable aléatoire. Cette proposition est particulièrement utile pour l'étude de la convergence en loi qui sert notamment dans la démonstration de la Loi Faible des Grands Nombres et du Théorème Central Limite. Elle nous permet également d'avoir tous les moments, par identification des coefficients du "développements limité". Concrètement cette proposition pourrait être placé avant le théorème d'injectivité (les deux démonstrations sont indépendantes l'une de l'autre, mais comme je l'ai dit, l'importance du théorème d'injectivité nous invite à le mettre en premier.
Petite remarque concernant la proposition intermédiaire, qui constitue une sorte de réciproque. Le fait qu'elle ne soit valable que pour n pair est curieux. Le contre-exemple cité est un peu "ad hoc" et il est intéressant de comprendre ce qui ne marche pas dans la démonstration. La preuve (je vous renvoie à [Ouvrard]) nécessite une interversion de limite avec l'espérance. Pour cela on utilise le lemme de Fatou (la limite inf existe ; on ne peut pas utiliser le théorème de Lebesgue car l'une des limites à considérer peut ne pas avoir de sens (rappelons au passage que ce n'est pas parce que l'on a une suite de fonction intégrable qui converge simplement vers une fonction intégrable que les conclusion au théorème de convergence dominé sont vraies)). Pour être utilisé (je parle du lemme de Fatou), le terme à l'intérieur de l'espérance doit être positif, ce qui n'est le cas que pour n pair...(Bon après ce n'est pas parce que l'on ne peut pas faire la même démonstration pour n impair que le résultat est faux, le contre-exemple est là pour ça.)
).
Ensuite on peut justifier l'utilité des formules d'inversion qui suivent en disant que la transformée de Fourier ne permet pas (au même titre que la fonction de répartition ou la densité (quand elle existe)) de calculer des probabilités.
Les démonstration de ces formules d'inversion se font facilement avec Fubini.
La proposition que suit établit une relation entre les propriétés de dérivabilité de la fonction caractéristique et l'existence de moment d'une variable aléatoire. Cette proposition est particulièrement utile pour l'étude de la convergence en loi qui sert notamment dans la démonstration de la Loi Faible des Grands Nombres et du Théorème Central Limite. Elle nous permet également d'avoir tous les moments, par identification des coefficients du "développements limité". Concrètement cette proposition pourrait être placé avant le théorème d'injectivité (les deux démonstrations sont indépendantes l'une de l'autre, mais comme je l'ai dit, l'importance du théorème d'injectivité nous invite à le mettre en premier.
Petite remarque concernant la proposition intermédiaire, qui constitue une sorte de réciproque. Le fait qu'elle ne soit valable que pour n pair est curieux. Le contre-exemple cité est un peu "ad hoc" et il est intéressant de comprendre ce qui ne marche pas dans la démonstration. La preuve (je vous renvoie à [Ouvrard]) nécessite une interversion de limite avec l'espérance. Pour cela on utilise le lemme de Fatou (la limite inf existe ; on ne peut pas utiliser le théorème de Lebesgue car l'une des limites à considérer peut ne pas avoir de sens (rappelons au passage que ce n'est pas parce que l'on a une suite de fonction intégrable qui converge simplement vers une fonction intégrable que les conclusion au théorème de convergence dominé sont vraies)). Pour être utilisé (je parle du lemme de Fatou), le terme à l'intérieur de l'espérance doit être positif, ce qui n'est le cas que pour n pair...(Bon après ce n'est pas parce que l'on ne peut pas faire la même démonstration pour n impair que le résultat est faux, le contre-exemple est là pour ça.)
(2) Transformée de Laplace)
Par la suite on s'intéresse à la transformée de Laplace. D'un point de vue résultats, elle n'apporte rien de plus et rien de moins que la transformation de Fourier (les propriétés sont analogues, ce que l'on pourra juste se contenter d'écrire à l'oral). En pratique, elle est beaucoup moins utilisée que la transformée de Fourier, car elle n'existe pas toujours sur un domaine "assez gros". En effet les conditions d'intégrabilité font que la transformée de Laplace n'est pas toujours bien définie (contrairement à la transformée qui est toujours bien définie sur 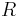 , ce qui lui vaut sa préférence). Cependant son avantage est qu'elle est est à valeur dans
, ce qui lui vaut sa préférence). Cependant son avantage est qu'elle est est à valeur dans 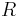 (elle est réelle analytique) et elle apparaît dans de nombreuses inégalités (via la relation d'ordre sur
(elle est réelle analytique) et elle apparaît dans de nombreuses inégalités (via la relation d'ordre sur 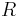 , donc contrairement à la transformée de Fourier, aucun intérêt de la définir dans
, donc contrairement à la transformée de Fourier, aucun intérêt de la définir dans 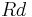 ), comme par exemple Chernoff ou Hoeffding (Partie III); ce qui justifie son étude. (Et puis aussi (paraît-il) peu de candidats en parle, alors cela démarque un peu plus.)
On notera que son développement dans un voisinage de 0 lui justifie sa notation et son nom de fonction génératrice des moments .
On donne ensuite des applications importantes comme la caractérisation d’une variable aléatoire réelle bornée par ses moments (la démonstration utilise la fonction caractéristique et le théorème d’injectivité, l’hypothèse bornée sert à majorer le reste intégrale du développement de Taylor à l’ordre n, pour montrer que celui-ci tend vers 0 quand n tend vers l’infini et obtenir l’analycité de la fonction caractéristique).
), comme par exemple Chernoff ou Hoeffding (Partie III); ce qui justifie son étude. (Et puis aussi (paraît-il) peu de candidats en parle, alors cela démarque un peu plus.)
On notera que son développement dans un voisinage de 0 lui justifie sa notation et son nom de fonction génératrice des moments .
On donne ensuite des applications importantes comme la caractérisation d’une variable aléatoire réelle bornée par ses moments (la démonstration utilise la fonction caractéristique et le théorème d’injectivité, l’hypothèse bornée sert à majorer le reste intégrale du développement de Taylor à l’ordre n, pour montrer que celui-ci tend vers 0 quand n tend vers l’infini et obtenir l’analycité de la fonction caractéristique).
(Partie II : Transformée de Fourier, produit de convolution et indépendance)
Cette partie est une conséquence immédiate de la partie précédente.
(1) Caractérisation de l’indépendance)
On obtient un critère d’indépendance de variables aléatoires en terme de fonctions caractéristiques (juste un mot de la démonstration : on montre au préalable que la transformée de Fourier du produit tensoriel de deux mesures est le produit des transformée de Fourier des mesures, le reste utilise Fubini et le théorème d’injectivité ( [OUVRARD] p106 et [Barbe-LEDOUX] p80)). On notera que l’on considère la fonction caractéristique d’un n-uplet de variables aléatoire, il fallait donc la définir dans 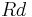 . Ce résultat sert beaucoup en pratique, à commencer avec la proposition qui suit qui donne une caractérisation de l’indépendance de variables aléatoires réelles bornées (l’hypothèse bornée donne , dans la démonstration, que la famille est sommable). On peut montrer que l’hypothèse bornée n’est pas nécessaire avec un exemple un peu adhoc que je n’ai pas mis dans le plan : pour Pas réussi à analyser (L’exécutable <code>texvc</code> est introuvable. Lisez math/README pour le configurer.): X=Y
. Ce résultat sert beaucoup en pratique, à commencer avec la proposition qui suit qui donne une caractérisation de l’indépendance de variables aléatoires réelles bornées (l’hypothèse bornée donne , dans la démonstration, que la famille est sommable). On peut montrer que l’hypothèse bornée n’est pas nécessaire avec un exemple un peu adhoc que je n’ai pas mis dans le plan : pour Pas réussi à analyser (L’exécutable <code>texvc</code> est introuvable. Lisez math/README pour le configurer.): X=Y
qui suit une loi de Cauchy on a la propriété qui est vérifié maisn’est pas indépendante d’elle même (car les seules variables aléatoires indépendantes d’elle-même sont les constante ps). Une deuxième application est la caractérisation de l’indépendance des composantes d’un vecteur gaussien (ce qui est faux dans le cadre non gaussien car cela voudrait dire que l’indépendance est caractérisée par la non corrélation).
(2) Loi de la somme de deux variables aléatoires indépendantes)
On rappelle oralement que le produit de convolution de deux mesures est la mesure image de leur produit tensoriel par l’application somme (on ne rappelle cette définition que maintenant car elle ne sert pas avant). On notera que dans le cas de deux variables aléatoires à densité on retrouve le produit de convolution usuel. On notera également (chose que je n’ai pas fais le jour de l’oral car c’est d’un intérêt limité) qu’une conséquence de cette proposition est que l’on peut approcher d’aussi près que l’on veut toute variable aléatoire réelle par une variable aléatoire à densité, en lui ajoutant une variable aléatoire à densité indépendante à valeur dans un voisinage suffisamment petit de zéros. On retrouve ici l’approche régularisante du produit de convolution. Il me semble que cela sert dans une preuve possible du théorème de Lévy à venir (dans la partie III) (cf [Barbe-Ledoux]). Une proposition importante est que la loi de la somme de deux variables aléatoires indépendantes est donné par le produit de convolution de leur loi (cf Théorème de Transfert). Cette proposition va de pair avec la suivante (qui est l’analogue probabiliste du fait que le Fourier du produit de convolution de deux fonctions est le produit des transformées de Fourier (et que l’on retrouve dans le cas de variables aléatoires à densité))…
(3) Transformée de Fourier d’une somme de variables aléatoires indépendantes)
qui donne un critère d’indépendance. Le point le plus important à noter est que compte tenu de l’injectivité de la transformée de Fourier, la transformée de Fourier fourni un moyen très efficace de déterminer la loi d’une somme finie de variables aléatoires indépendantes. (Dont l’importance est rappelé en Partie III avec les théorèmes limites). On notera que l’on a un résultat analogue avec la transformée de Laplace. On donne ensuite des exemples et des applications. Le théorème de Bernstein donne une condition suffisante, d’apparence très peu exigeante, pour que deux variables aléatoires réelles soient gaussiennes (c’est un théorème notable mais je ne crois pas qu’il serve énormément en pratique (à vérifier…)). La dernière application est certainement la plus importante puisqu’elle est très utile en statistique. Elle caractérise elle aussi le caractère gaussien mais cette fois ci en terme d’indépendance de moyenne et de variance empirique (qui sont des estimateurs), (et pour que cela ai un sens on suppose donc que les Xi sont de carrés intégrables). Un mot de la démonstration : elle est technique, on montre que la fonction caractéristique vérifie une certaine équation différentielle dont la solution est une gaussienne (aucun intérêt de le citer à l’oral mais c’est toujours bien de connaître les outils utilisés). Dans toute cette partie (et dans celle qui suit aussi) le théorème d’injectivité est sous jasent et joue un rôle crucial.
(Partie III : Etude du comportement asymptotique)
(1) Convergence en loi et convergence des fonctions caractéristique)
On peut rappeler oralement que la convergence en loi est donnée par la convergence étroite des suites de mesure (attention dans la définition c’est pour toutes fonctions continues et non pas boréliennes). (Il est aussi possible de prendre comme définition la convergence simple des fonctions de répartition en tout point de continuité de la fonction de répartition limite). Au même titre que la fonction de répartition, on caractérise la convergence en loi en terme de convergence simple de fonctions (ici les fonctions caractéristiques). Attention dans le premier théorème on suppose que la limite est une fonction caractéristique. En générale, une suite de fonctions caractéristique ne converge pas nécessairement vers une fonction caractéristique, le contre exemple du plan est la pour l’illustrer. On en vient alors au Théorème de Lévy qui donne une condition suffisante pour que la limite d’une fonction caractéristique soit une fonction caractéristique. Attention la démonstration du Théorème de Lévy fait appel à des notions profondes d’Analyse Fonctionnelle. La puissance de la Transformée de Fourier vient du fait qu’elle transforme le produit de convolution des mesures en produit de fonction, et que les propriétés de convergence en mesure se traduisent en terme de convergence simple de leur transformée de Fourier. Toute cette étude va nous servir à démontrer des nombreux théorèmes limite où l’on doit déterminer la convergence d’une somme de variables aléatoires indépendantes.
(2) Application : Théorème limites)
C’est ainsi que l’on peut démontrer facilement la Loi Faible (attention et pas la forte relative à la convergence presque sûre) des Grands Nombres. Cette démonstration est énoncé dans le cas d’une convergence en probabilité, car la convergence en loi vers une variable aléatoire constante presque sûrement est aussi une convergence presque sûre (savoir le redémontrer rapidement). On notera que la démonstration, contrairement à celle utilisant l’inégalité de Bienaymé Tchebychev, ne nécessite pas de supposer les variables aléatoires Xi de carré intégrable. On démontre grâce aux outils développé le TCL (que l’on énonce dans le cas réel, mais qui se généralise dans 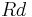 , la formulation est mise sous une forme qui reste également valable dans
, la formulation est mise sous une forme qui reste également valable dans 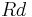 (on notera aussi que la démonstration de la généralisation nécessite le TCL dans le cas réel).
On énonce également les Inégalités de Chernoff et de Hoeffding. Comme on la signalé plus haut, la transformé de Laplace est utilisé pour le cas réel, pour des inégalités. En soi les outils développé ne sont pas déterminant, mais ces inégalité font apparaître la transformée de Laplace. J’ai mis beaucoup de temps avant de me décider dans l’ordre dans lequel j’allais les mettre, et si elles devaient être placées avant ou après le TCL. J’ai choisi l’ordre du plan car l’inégalité de Chernoff nous renseigne un peu plus sur la Loi de Grands Nombres ([COT] p164) et l’Inégalité de Hoeffding établit que la vitesse de convergence de la LGN est exponentielle (dans le cas d’une suite de variables aléatoires réelle bornées ps et centrées), cas donc un cas particulier du TCL avec un résultat plus précis. On termine avec le théorème de Poisson (cas particulier d’un Théorème plus général sit des évènements rares (et qui tire son nom du fait que l’on s’intéresse à une suite d’évènements de probabilité de plus en plus petite) et le Théorème de Karl Pearson, important en statistiques puisqu’il légitime le test du Chi-deux.
(on notera aussi que la démonstration de la généralisation nécessite le TCL dans le cas réel).
On énonce également les Inégalités de Chernoff et de Hoeffding. Comme on la signalé plus haut, la transformé de Laplace est utilisé pour le cas réel, pour des inégalités. En soi les outils développé ne sont pas déterminant, mais ces inégalité font apparaître la transformée de Laplace. J’ai mis beaucoup de temps avant de me décider dans l’ordre dans lequel j’allais les mettre, et si elles devaient être placées avant ou après le TCL. J’ai choisi l’ordre du plan car l’inégalité de Chernoff nous renseigne un peu plus sur la Loi de Grands Nombres ([COT] p164) et l’Inégalité de Hoeffding établit que la vitesse de convergence de la LGN est exponentielle (dans le cas d’une suite de variables aléatoires réelle bornées ps et centrées), cas donc un cas particulier du TCL avec un résultat plus précis. On termine avec le théorème de Poisson (cas particulier d’un Théorème plus général sit des évènements rares (et qui tire son nom du fait que l’on s’intéresse à une suite d’évènements de probabilité de plus en plus petite) et le Théorème de Karl Pearson, important en statistiques puisqu’il légitime le test du Chi-deux.