103 -- Conjugaison dans un groupe. Exemples de sous-groupes distingués et de groupes quotients. Applications. : Différence entre versions
| Ligne 68 : | Ligne 68 : | ||
[[Category:leçon d'algèbre]] | [[Category:leçon d'algèbre]] | ||
[[Category:leçon sur les groupes]] | [[Category:leçon sur les groupes]] | ||
| − | |||
Version du 22 septembre 2019 à 17:50
Sommaire
Plans
Plan scanné de l'année 2012-2013
Plan scanné de l'année 2013-2014
Plan scanné de l'année 2014-2015
Plan scanné de l'année 2015-2016
Plan scanné de l'année 2016-2017
Plan scanné de l'année 2017-2018
Medley de rapports de jury
Des exemples et applications en géométrie élémentaire sont nécessaires.
La notion de produit semi-direct n’est plus au programme, mais lorsqu’elle est utilisée il faut savoir la définir proprement
En général le stabilisateur d'un élément n'est pas un sous-groupe distingué contrairement à ce qu'a pu entendre le jury.
Les candidats parlent de groupes simples et de sous-groupe dérivé ou de groupe quotient sans savoir utiliser ces no- tions. Il faudrait savoir par exemple que
- tout morphisme de source un groupe simple est soit injectif soit trivial.
- dans un groupe simple, toute réunion de classes de conjugaison non triviale engendre le groupe (par exemple les éléments de la forme x 2 y x).
- tout morphisme d’un groupe G vers un groupe abélien se factorise via G ab := G/D(G).
Il faut bien connaître le cas du groupe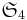 
, notamment 
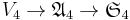et faire le lien avec le tétraèdre.
Autre plan
Le plan que Perrine et moi avons fait pour cette leçon :
I) Conjugaison et Groupe quotient
Naturellement mené par la question : à quelle condition un sous-groupe peut-il être noyau d'un morphisme ?
1- conjugaison et sous-groupes distingués (exemple des permutations de même profil)
2 - classe à gauche (permet de montrer Lagrange et Frobénius - F-G-N oraux X-ENS algèbre 1 p. 48)
3 - groupe quotient (factorisation de morphismes...)
II) Simplicité et résolubilité
Notions aux implications importantes via Galois pour la résolution par radicaux des polynômes et la résolution par quadrature des équations différentielles.
Théorèmes de Sylow, groupe dérivé, Lie-Kolchin (Chambert-Loir "a field guide to algebra" p. 98), suite de Jordan-Hölder (Delcourt "Théorie des groupes")
III) Devissage de groupes
Autrement dit comment se ramener à des groupes plus petits pour étudier les propriétés du groupe de départ.
Théorème chinois et structure des abéliens de type fini. La caractérisation du produit direct(avoir deux sous-groupes distingués H, K avec HK=G et H
K={e}) amène la définition du produit semi-direct et sa caractérisation (idem mais K n'est pas distingué). Ceci permet de lister les groupes d'ordre 8 ou 12 (Delcourt p.99)
