Lemme de Morse : Différence entre versions
De AgregmathKL
m (biblio correcte) |
m |
||
| Ligne 1 : | Ligne 1 : | ||
| − | Un changement de coordonnée pour les applications de classe <math>\mathcal{C}^3</math>. | + | Un changement de coordonnée pour les applications de classe <math>\mathcal{C}^3</math>, et une application à l'étude de la topologie de l'ensemble des formes quadratiques sous l'action du groupe linéaire. |
| − | + | ||
== Recasement :== | == Recasement :== | ||
* [[131 -- Formes quadratiques sur un espace vectoriel de dimension finie. Orthogonalité, isotropie. Applications.]] | * [[131 -- Formes quadratiques sur un espace vectoriel de dimension finie. Orthogonalité, isotropie. Applications.]] | ||
| Ligne 7 : | Ligne 6 : | ||
* [[218 -- Applications des formules de Taylor.]] | * [[218 -- Applications des formules de Taylor.]] | ||
| − | == Développement == | + | == Développement : Lemme de Morse == |
=== Version 2010/2011 :=== | === Version 2010/2011 :=== | ||
| Ligne 18 : | Ligne 17 : | ||
Pdf : [[Fichier:Pdf.png|alt=Tex|link=Média: dvt_morse.pdf |24px]] | Pdf : [[Fichier:Pdf.png|alt=Tex|link=Média: dvt_morse.pdf |24px]] | ||
| − | == | + | == Topologie de l'ensemble des formes quadratiques == |
Le lemme de réduction <math>\mathcal{C}^1</math> des formes quadratiques proches peut s'interpréter en termes topologiques : | Le lemme de réduction <math>\mathcal{C}^1</math> des formes quadratiques proches peut s'interpréter en termes topologiques : | ||
[[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Comp_conn.pdf | Composantes connexes de l'ensemble des formes quadratiques non dégénérées.]] | [[Fichier:Pdf.png|alt=Pdf|link=|24px]] [[Média:Comp_conn.pdf | Composantes connexes de l'ensemble des formes quadratiques non dégénérées.]] | ||
| − | + | (ce n'est pas une application du lemme de morse à proprement parler). | |
== Références == | == Références == | ||
[[Rouvière | François Rouvière, ''Petit guide de calcul différentiel'']] | [[Rouvière | François Rouvière, ''Petit guide de calcul différentiel'']] | ||
Version du 2 juin 2012 à 15:38
Un changement de coordonnée pour les applications de classe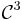 
, et une application à l'étude de la topologie de l'ensemble des formes quadratiques sous l'action du groupe linéaire.
Sommaire
Recasement :
- 131 -- Formes quadratiques sur un espace vectoriel de dimension finie. Orthogonalité, isotropie. Applications.
- 214 -- Théorème d'inversion locale, théorème des fonctions implicites. Exemples et applications.
- 215 -- Applications différentiables définies sur un ouvert de Rn. Exemples et applications.
- 218 -- Applications des formules de Taylor.
Développement : Lemme de Morse
Version 2010/2011 :
Version 2011/2012 :
Source 
: Lemme de Morse
Pdf : 
Topologie de l'ensemble des formes quadratiques
Le lemme de réduction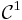 
des formes quadratiques proches peut s'interpréter en termes topologiques :
Composantes connexes de l'ensemble des formes quadratiques non dégénérées.
(ce n'est pas une application du lemme de morse à proprement parler).
