Sous-groupes compacts de GL n : Différence entre versions
(Page créée avec « Ce développement montre qu'un sous-groupe compact de <math>GL_n</math> est un sous-groupe d'un groupe orthogonal pour un certain produit scalaire. == Remarques == Le dével... ») |
m (→Le développement : dev2012) |
||
| Ligne 12 : | Ligne 12 : | ||
=== Version 2012 === | === Version 2012 === | ||
| + | [[Fichier:Pdf.png|alt=Tex|link=|24px]] [[Média:Sg_compact_GLn_2012.pdf | Sous-groupes compacts de <math>GL_n</math>]] | ||
== Recasements == | == Recasements == | ||
Version du 26 novembre 2011 à 20:05
Ce développement montre qu'un sous-groupe compact de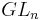 
est un sous-groupe d'un groupe orthogonal pour un certain produit scalaire.
Sommaire
Remarques
Le développement est long et nécessite de nombreux résultats puissants. Entre autre il semble impossible de le faire tenir en 15 minutes sans admettre le théorème de Carathéodory sur l'enveloppe convexe en dimension finie.
Un énoncé équivalent stipule que les sous-groupes compacts de 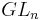sont exactement les sous-groupes de 
à conjugaison près. Ce résultat est à replacer dans le contexte de la richesse de la géométrie euclidienne en dimension finie qui est très bien développé dans Alessandri.
Le développement
Version 2011
Version 2012
Recasements
(D) signale les développements de l'option informatique.
Algèbre
- 106 -- Groupe linéaire d'un espace vectoriel de dimension finie E, sous-groupes de GL(E). Applications. (D)
- 119 -- Exemples d'actions de groupes sur des espaces de matrices.
- 131 -- Formes quadratiques sur un espace vectoriel de dimension finie. Orthogonalité, isotropie. Applications. (D)
- (133 -- Endomorphismes remarquables d'un espace vectoriel euclidien de dimension finie.) (D)
Analyse
Il est à noter que ce développement n'est pas à proprement parler une "utilisation de la notion de compacité".
- 206 -- Théorèmes de point fixe. Exemples et applications. (D)
- (203 -- Utilisation de la notion de compacité.) (D)
- (229 -- Fonctions monotones. Fonctions convexes. Exemples et applications.) (D)
Références
- Alessandri : Thèmes de Géométrie, p141 et 160
